graphing exponential functions worksheet pdf
Exponential functions, in the form y = ab^x, are essential in mathematics. Graphing them helps visualize growth and decay patterns, identifying key features like asymptotes and direction.
1.1 What Are Exponential Functions?
Exponential functions are mathematical expressions of the form y = ab^x, where ‘a’ and ‘b’ are constants, and ‘x’ is the variable. These functions describe growth or decay, with ‘b’ determining the rate. When b > 1, the function grows rapidly, while 0 < b < 1 results in decay. They are fundamental in modeling real-world phenomena like population growth and radioactive decay.
1.2 Importance of Graphing in Understanding Exponential Functions
Graphing exponential functions provides a visual representation, making it easier to interpret growth and decay patterns. It helps identify key components like asymptotes, intercepts, and transformations. By plotting points, students can observe how changes in the base or coefficient affect the graph, enhancing their understanding of these functions and their real-world applications.

Key Concepts for Graphing Exponential Functions
Understanding the general form y = ab^x, identifying asymptotes, and distinguishing between growth and decay are crucial for accurately graphing exponential functions and interpreting their behavior.
2;1 Understanding the General Form of Exponential Functions (y = ab^x)
The general form of an exponential function is y = ab^x, where ‘a’ is the y-intercept, ‘b’ is the growth or decay factor, and ‘x’ is the exponent. If b > 1, the function grows; if 0 < b < 1, it decays. This form is fundamental for sketching graphs and solving problems in exponential function worksheets.
2.2 Identifying Asymptotes, Domain, and Range
Exponential functions have a horizontal asymptote, typically y = 0, which the graph approaches but never touches. The domain of y = ab^x is all real numbers, while the range is (0, ∞) for growth or (-∞, 0) for decay. Identifying these elements is crucial for accurately sketching and analyzing exponential graphs in worksheets and problems.
2.3 Distinguishing Between Exponential Growth and Decay
Exponential growth occurs when the base b > 1, causing the function to rise rapidly. Conversely, decay happens when 0 < b < 1, leading the function to decrease over time. Worksheets often include problems that require identifying these behaviors, helping students understand the fundamental differences and their real-world implications, such as population growth or radioactive decay scenarios.
Types of Exponential Functions
Exponential functions can have different bases, such as natural (base e) or base 10. Each type has unique properties and applications, making them essential for various real-world calculations and modeling scenarios.
3.1 Natural Exponential Functions (Base e)
Natural exponential functions use the base e (approximately 2.71828), a fundamental constant in mathematics. These functions, expressed as y = ae^x, are crucial in modeling continuous growth and decay, such as population growth and radioactive decay. They are widely used in calculus and real-world applications due to their unique properties and versatility in representing exponential changes over time.
3.2 Exponential Functions with Base 10
Exponential functions with base 10, expressed as y = a*10^x, are commonly used in applications like population growth and resource depletion. These functions are straightforward to graph due to their familiar base, making them ideal for teaching exponential concepts. They have a horizontal asymptote at y=0, a domain of all real numbers, and a range of positive values, growing rapidly for positive x and decaying for negative x.
Transformations of Exponential Functions
Transformations like horizontal shifts, vertical shifts, stretching, and reflecting alter the graph’s appearance. These modifications help model real-world scenarios, enhancing the function’s applicability and complexity.
4.1 Horizontal and Vertical Shifts
Horizontal shifts occur when x is replaced by (x ⸺ h) in the function, moving the graph left or right. Vertical shifts happen when a constant is added or subtracted to the function, moving the graph up or down. These shifts are crucial for accurately modeling real-world data and understanding function transformations.
4.2 Stretching and Reflecting Exponential Functions
Stretching an exponential function vertically is achieved by multiplying the function by a constant factor. Reflecting the graph over the x-axis occurs when the function is multiplied by a negative coefficient. These transformations alter the graph’s shape and orientation but retain the exponential behavior, helping model real-world phenomena like population decline or financial losses.

Steps to Graph Exponential Functions
Identify the asymptote, plot key points, and determine if the function grows or decays to accurately sketch exponential functions.
5.1 Identifying the Asymptote
The asymptote of an exponential function is a horizontal line that the graph approaches but never touches. For y = ab^x, the asymptote is typically y = 0. Identifying it helps in sketching the graph accurately, as it serves as a boundary for the function’s behavior. This step is crucial for understanding the function’s growth or decay patterns.
5.2 Plotting Key Points
Plotting key points, such as intercepts and integer values, helps in accurately sketching exponential functions. For example, identifying points like (0, a) and (1, ab) provides a clear starting point. These points guide the shape of the graph, making it easier to visualize the function’s behavior and determine if it exhibits growth or decay over time.
5.3 Determining the Direction of Growth or Decay
To determine if an exponential function exhibits growth or decay, examine the base ‘b’. If b > 1, the function grows exponentially as x increases. If 0 < b < 1, it decays. Analyzing the graph's trend over time helps confirm this behavior, ensuring accurate visualization and interpretation of the function's growth or decay pattern.

Common Challenges in Graphing Exponential Functions
Students often struggle with identifying asymptotes and distinguishing between exponential growth and decay. Misinterpreting the base ‘b’ and scale changes can lead to graphing errors and misanalysis.
6.1 Misidentifying the Asymote
Misidentifying the asymptote is a common issue when graphing exponential functions. Students often confuse it with the x-axis or y-axis, leading to incorrect graph shapes. This error stems from rushing to plot points without understanding the function’s behavior. For y = ab^x, the asymptote is y = 0, but confusing it with other lines can misrepresent growth or decay patterns, affecting the entire graph’s accuracy and interpretation.
6.2 Confusing Exponential Growth with Decay
Confusing exponential growth with decay is another common mistake. This happens when students misinterpret the base of the function. If the base ( b ) is greater than 1, the function grows, while values of ( b ) between 0 and 1 indicate decay. Mixing these concepts leads to incorrect graphical representations and misunderstandings of real-world applications, such as population growth or radioactive decay.

Practice Worksheets for Graphing Exponential Functions
Downloadable PDF worksheets provide exercises for graphing exponential functions, including plotting equations, identifying asymptotes, and distinguishing growth from decay, suitable for various grade levels and skill sets.
7.1 Downloadable PDF Worksheets
Downloadable PDF worksheets on graphing exponential functions offer a variety of exercises, including graphing equations, identifying asymptotes, and determining growth or decay. These worksheets are designed for students to practice and master the concepts of exponential functions. They are available for different grade levels and can be printed for convenient use in the classroom or at home.
7.2 Examples of Problems in Worksheets
Worksheets on graphing exponential functions include problems like sketching graphs of y = ab^x, identifying asymptotes, and determining whether functions exhibit growth or decay. Students are also asked to write equations from graphs and match functions to their transformations. Examples include tasks like graphing y = 3x + 2 or identifying anchor points for functions like y = 4(2x).
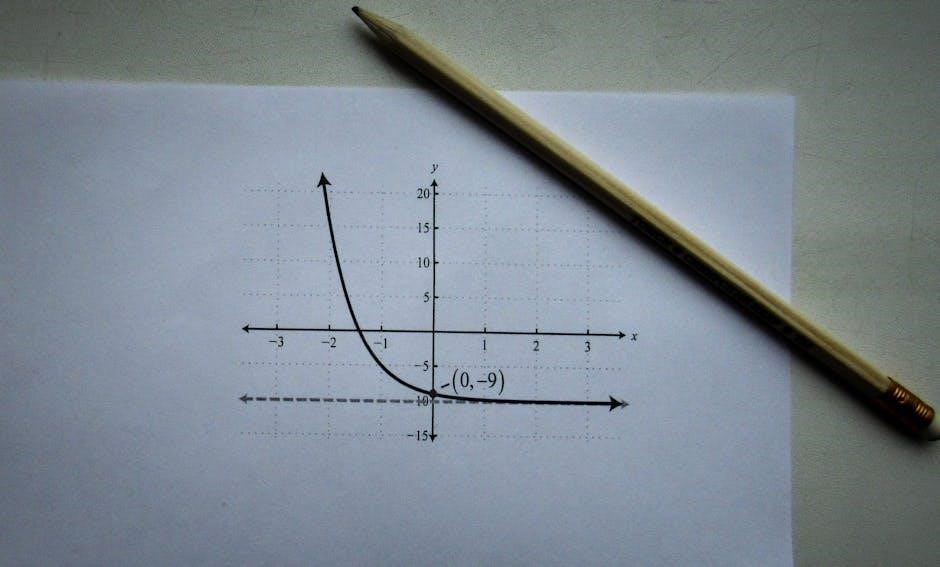
Tips for Mastering Graphing Exponential Functions
Use anchor points to plot key coordinates and analyze transformations. Regular practice with worksheets ensures fluency in identifying asymptotes and distinguishing growth from decay patterns effectively.
8.1 Using Anchor Points
Anchor points simplify graphing by plotting key coordinates. Identify the y-intercept (0, a) and use exponential behavior to find additional points. This method helps in sketching precise graphs, ensuring accuracy in growth and decay visualization. Regular practice with graphing exponential functions worksheet PDFs reinforces this technique effectively for better understanding and mastery of exponential functions.
8.2 Analyzing Transformations
Transformations alter the graph’s appearance without changing its fundamental exponential nature. Horizontal shifts move the graph left or right, while vertical shifts move it up or down. Stretching or compressing vertically changes the growth rate, and reflecting over the x-axis inverts the function. Practicing with graphing exponential functions worksheet PDFs helps master these adjustments for accurate graph sketching and interpretation.

Real-World Applications of Exponential Functions
Exponential functions model real-world phenomena like population growth and radioactive decay. Graphing these functions helps visualize and predict future trends, making them essential in science and finance.
9.1 Population Growth
Exponential functions are crucial in modeling population growth, where the rate of increase accelerates over time. For instance, bacteria growth follows an exponential pattern, doubling rapidly under ideal conditions. Similarly, animal populations can exhibit exponential growth when resources are abundant; Graphing these functions helps ecologists predict future trends and understand environmental impacts, making it a vital tool in conservation and resource management strategies.
9.2 Radioactive Decay
Exponential functions are used to model radioactive decay, where unstable atoms lose energy over time. The decay process follows an exponential pattern, with the material’s quantity decreasing at a constant rate. Graphing these functions helps scientists visualize and predict the remaining material over time, emphasizing the concept of half-life, a critical factor in nuclear physics and environmental science applications.

Assessing Understanding
Exponential functions model radioactive decay, where unstable materials lose energy over time. The decay follows an exponential pattern, with the material’s quantity decreasing at a constant rate. Graphing these functions illustrates the decay process, emphasizing the concept of half-life, a critical factor in nuclear physics and environmental science applications.
10.1 Multiple-Choice Questions
Multiple-choice questions are an effective way to assess understanding of exponential functions. They test the ability to evaluate functions, identify asymptotes, and distinguish between growth and decay. These questions also clarify common misconceptions, such as misidentifying the base or confusing transformation effects. Regular practice with multiple-choice exercises helps reinforce key concepts and ensures mastery of graphing techniques.
10.2 Short-Answer Questions
Short-answer questions require students to provide concise, detailed responses about exponential functions. They assess the ability to evaluate functions, identify asymptotes, and analyze transformations. These questions often ask for specific examples or explanations, such as determining whether a function represents growth or decay or calculating key points on a graph. They ensure a deeper understanding of exponential behavior and its graphical representation.

Additional Resources
Explore recommended websites and video tutorials for in-depth learning. These resources provide interactive examples, step-by-step guides, and practice problems to master graphing exponential functions effectively.
11.1 Recommended Websites
Visit Khan Academy and Mathway for detailed guides on graphing exponential functions. Algebra.com offers interactive tools, while GeoGebra provides visual simulations. These sites are ideal for practice and understanding complex concepts through examples and step-by-step solutions.
11.2 Video Tutorials
YouTube channels like 3Blue1Brown and Crash Course offer engaging video tutorials on graphing exponential functions. Websites such as Khan Academy and Math Antics provide step-by-step explanations. These resources are perfect for visual learners and supplement practice worksheets with clear, interactive lessons on exponential growth, decay, and transformations.
